Beispielaufgaben
Die folgende Aufgabe stammt aus den KMK-Bildungsstandards und ist der Leitidee „Muster und Strukturen" zuzuordnen. Im Einzelnen geht es bei den unterschiedlichen, jedoch zusammenhängenden Aufgabenstellungen darum,
- mathematische Zusammenhänge zu erkennen und Vermutungen zu entwickeln,
- Begründungen zu suchen und nachzuvollziehen,
- für das Bearbeiten mathematischer Probleme geeignete Darstellungen zu entwickeln, auszuwählen und zu nutzen,
sowie inhaltlich darum, Gesetzmäßigkeiten in geometrischen (und arithmetischen) Mustern zu erkennen, zu beschreiben und fortzusetzen:
|
Aufgabenstellung: 1. Aufgabe: Dieses Muster beginnt mit einem Dreierstreifen. Zeichne das 4. Bild. (Anforderungsbereich I)
2. Aufgabe: Bestimme die Anzahl der Kästchen vom 15. Bild ohne zu zeichnen. (Anforderungsbereich II) 3. Aufgabe: Jens zeichnet dieses Muster immer weiter. Kann es sein, dass er auf diese Weise ein fertiges Bild mit genau 125 Kästchen zeichnet? (Anforderungsbereich II) Ja _____ Nein _____ Begründung: ________________________________
4. Aufgabe: Lisas Muster beginnt mit einem Dreierstreifen wie in der 1. Aufgabe. Michael fängt mit einem Viererstreifen an. Sie stellen fest, dass einige Bilder gleich viele Kästchen haben. Wie viele Kästchen haben diese Bilder? Schreibe vier Möglichkeiten auf. (Anforderungsbereich III) |
Beispielaufgabe „Würfeln"
Diese Aufgabe ist der Leitidee „Daten, Zufall und Wahrscheinlichkeit" angehörig. Es geht darum,
- Lösungsstrategien zu entwickeln und zu nutzen,
- mathematische Zusammenhänge zu erkennen und Vermutungen zu entwickeln,
sowie inhaltlich darum, Gewinnchancen bei einfachen Zufallsexperimenten einzuschätzen und Grundbegriffe zu kennen.
Wie auch beim Beispiel „Kästchenmuster" ist wieder eine enge Verbindung zur Kompetenz des Problemlösens gegeben.
|
1. Aufgabe: Bei einem Spielwürfel ist die Summe der gegenüberliegenden Augenzahlen stets 7. (AB I) Also liegt 3 gegenüber von ___ liegt ___ gegenüber von ___ liegt ___ gegenüber von ___ .
2. Aufgabe: Stell dir vor, du würfelst mit einem Spielwürfel 5 mal und addierst die Zahlen. (AB II) Die kleinstmögliche Summe ist: ________ Die größtmögliche Summe ist: ________
3. Aufgabe: Stell dir vor, du würfelst mit zwei Spielwürfeln. (AB II) Bei jedem Wurf addierst du die gewürfelten Augenzahlen der beiden Würfel. Welche Summen sind möglich? Schreibe alle auf.
4. Aufgabe: Beim Würfeln mit zwei Spielwürfeln wird die Summe 7 wesentlich häufiger gewürfelt als die Summe 12. Woran liegt das? (AB III)
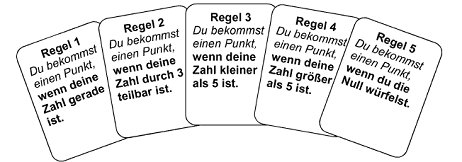
5. Aufgabe: Du spielst mit Freunden mit einem Spielwürfel. Jeder der Spieler darf sich eine Regel aussuchen, nach der er seine Punkte bekommt. (AB III)
Du möchtest möglichst viele Punkte haben. Welche Regel würdest du wählen? Warum? |
Weitere Aufgabenbeispiele: Siehe unter https://arbeitsplattform.bildung.hessen.de/fach/sinus_grundschule//aufgabe/